Вероятностное распределение Пуассона в хоккее. Часть 1

При проведении рационального анализа какого-либо вида спорта каждый раз почти неизбежно возникает вопрос о влиянии показателей или тактик на вероятности исходов. Как следствие, модель, прогнозирующая вероятности исходов – это своеобразный Святой Грааль спортивного анализа. Многих игроков интересует, как делать грамотные ставки на хоккей. Для хоккея существует несколько моделей, которые дают адекватные результаты, включая основные и обобщенные методы Пифагора, но эти методы являются эмпирическими, им не хватает теоретической основы. Данное исследование направлено на разработку модели, хорошо подкрепленной статистической теорией и превосходящей любой из существующих методов.

Распределение Пуассона для ставок на хоккей 

С французского “пуассон” переводится как “рыба”, однако наше исследование посвящается вовсе не рыбе и не рыбалке. В статистике Пуассон – это описание вероятностей, и данное исследование посвящается применению распределения Пуассона в хоккее с шайбой (с добавлением нескольких штрихов других распределений вероятностей). Вы узнаете, как проявляется распределение Пуассона в хоккее и как его можно использовать для оценки вероятностей определенных событий. В частности, я исследую распределения вероятностей для двух конкурирующих переменных Пуассона и рассчитаю вероятности исходов выигрыша в хоккейном матче конкурирующего Пуассона с учетом склонностей к забитым и пропущенным голам. Попутно я предлагаю рассмотреть простую формулу, учитывающую Z голы, для расчета вероятностей по Пуассону. И, наконец, поскольку применение распределения Пуассона к хоккею имеет свои ограничения, я расширю базовую теорию, чтобы рассмотреть пару структурных особенностей хоккея.

Что такое "распределение вероятностей"?

Распределение вероятностей математически описывает вероятность того, что случайная величина (Х) примет определенное значение (х). Существует множество распределений вероятностей. Некоторые из них, к примеру, нормальное распределение, относятся к непрерывным переменным (таким как время, вес, длина и т.д.). Другие относятся к дискретным переменным, которые обнаруживаются, если мы считаем такие вещи, как голы в хоккейном матче. И когда у вас происходит множество дискретных событий, вы можете использовать дискретное распределение для описания вероятностей.

Любой, кто прослушал курс статистики, обязательно встречался с Биномиальным распределением. В биномиальном процессе события происходят с успехом или неудачей. Классический пример Биномиального процесса – бросок монеты. Если мы подбросим монету 10 раз, количество выпавших орлов будет следовать Биномиальному распределению вероятностей. Если же мы повторим этот эксперимент множество раз, биномиальное предсказание количества орлов будет подтверждено экспериментальным путем.

В Пуассоновском процессе события имеют тенденцию происходить во времени случайным образом, при этом неважные события многочисленны или неизвестны. Например, количество ударов молнии в регионе за период времени – это процесс Пуассона. Если происходящее событие является редким, случайным, и не зависит от истории предыдущих событий – оно относится к процессу Пуассона, а его вероятности могут быть описаны распределением вероятностей Пуассона.

Вероятность того, что переменная Пуассона X примет значение x, равна:

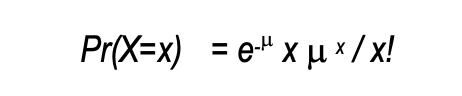
где параметр μ демонстрирует тенденцию к возникновению события.

Ожидаемое количество событий – это свойство распределения Пуассона. Иногда μ записывается как λt, где λ являет собой интенсивность пуассоновского процесса в единицу времени. Здесь и далее я предполагаю, что t=1, и буду использовать μ для описания ожидаемого количества событий в 1 единицу времени.

Ниже приведена выборка вероятностей Пуассона для μ = 2,57. Это говорит о том, что при среднем количестве в 2,57 событий, происходящих за период времени, вероятность ровно 3 событий составляет 0,21639.

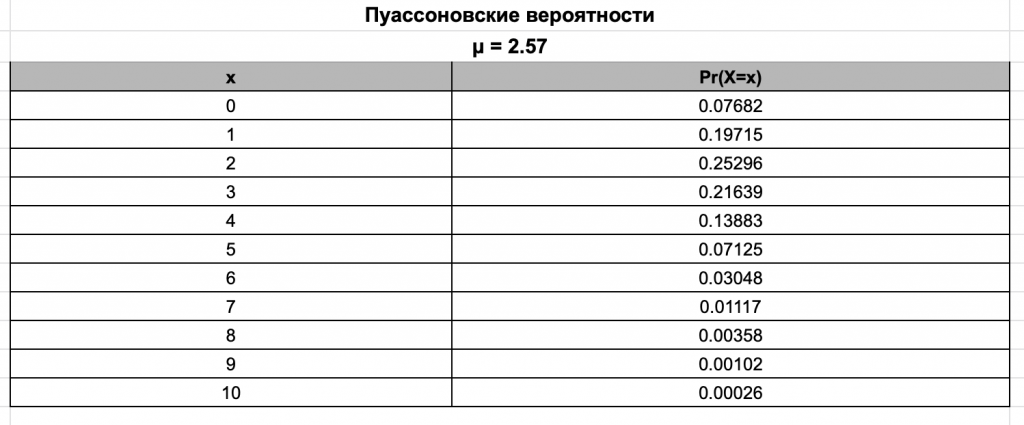
В Excel распределение Пуассона реализовано следующим образом:

Pr (X = x) = ПУАССОН (x ,μ, ЛОЖЬ) для плотности вероятности; 

Pr (X≤x) = ПУАССОН (x, μ, ИСТИНА) для кумулятивной вероятности.

Ценность вероятностной модели заключается в том, что она дает вам ориентир, который вы можете использовать для прогнозирования. Это полезно и само по себе, но вы также можете сравнить результаты с прогнозами, чтобы ответить на вопрос: «Получил ли я то, что ожидал?» Если вы не получаете ожидаемого, это говорит о том, что либо параметр был неправильно оценен, либо одно или несколько общих условий Пуассона не выполняются. Любой из этих выводов может многое рассказать нам о рассматриваемых обстоятельствах.

Математика хоккея

Как Пуассон связан с хоккеем? Подсчет голов в хоккейном матче по сути является Пуассоновским процессом. Тай-брейки в некоторых видах спорта можно считать биномиальными, но хоккей – это Пуассон. Далее мы с вами выясним, что хоккей действительно является достаточно Пуассоновским, но для начала проясним пару моментов. Также вам нужно будет узнать о важном ограничении на применение распределения Пуассона, о котором я расскажу позже.

Момент №1

Существует 3 основных требования к процессу Пуассона: события должны быть редкими, случайными и не должны обладать памятью.

• Не иметь памяти в данном случае означает, что вероятность события не меняется при наступлении предыдущего события. Если бы голы естественным образом возникали в кластерах, в процессе была бы некоторая «память»; такими свойствами, похоже, может обладать бейсбол, но вот хоккей – нет.
• Редкость означает, что для мероприятия существует множество разных возможностей, но развивается лишь ограниченный ряд событий. Как показывает практика, событие можно считать редким, когда количество потенциальных событий превышает 100, а вероятность события составляет менее 10%. Для того, чтобы гол был забит, требуется всего несколько секунд. Потенциально создается очень много моментов для взятия ворот (не путайте моменты с ударами по воротам), но в действительности очень немногие из них действительно становятся голом. Голы являются редкими.
• Случайность означает, что события разбросаны во времени без видимой закономерности. Чтобы проверить случайность, вы должны разделить игру на рациональные части и подсчитать голы по частям. Статистическим тестом для них является нормальность подсчетов. Если подсчеты распределяются нормально, мы заключаем, что наблюдаем случайный процесс. Голы в основном случайны, но есть одно существенное исключение.

Хоккейная статистика. Когда голы не случайны?

Ниже приведены три гистограммы, показывающие распределение количества голов в сезоне 2003-2004 по минутам в каждом из трех периодов игры.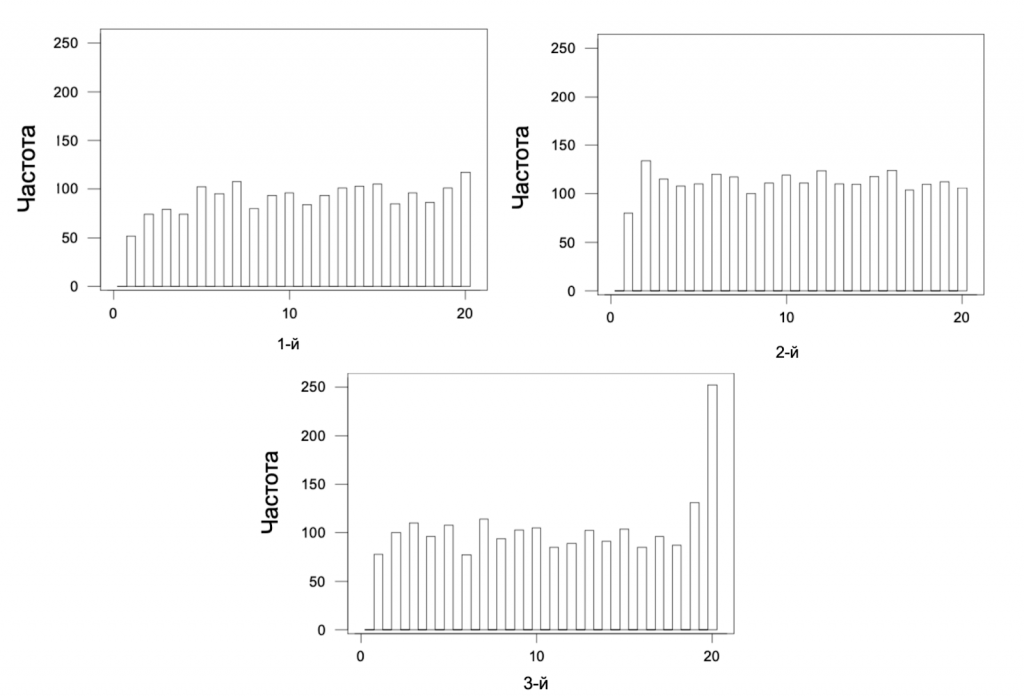



Я проигнорировал овертаймы, поскольку их немного сложнее анализировать и они ничего не добавят в мои наблюдения. В данных из этих гистограмм присутствует несколько закономерностей, но только одна из них является статистически значимой. Вот эти закономерности:

1. Во всех трех периодах в первую минуту игры результативность самая низкая.
2. В первом периоде наблюдается небольшая тенденция к росту в течение первых 5 минут игры с последующим стабильным рисунком.
3. В третьем периоде результативность кажется достаточно стабильной, исключение – результативность в последние 2 минуты игры.
4. Результативность зависит от периода.

Используем аналитику хоккейных матчей

Паттерн «низкая результативность первой минуты периода» объясняется сразу несколькими факторами. Во-первых, команды еще не разогрелись перед игрой, во-вторых – они проявляют определенную осторожность в начале периода. Но главной причиной является тот факт, что первая минута периода начинается с вбрасывания шайбы, в результате чего первые несколько секунд потенциальной атаки теряются, чего не происходит в остальные 19 минут периода на постоянной основе. Тест на нормальность находит эти данные «странными», но все же делает вывод, что они являются случайными.

Что касается паттерна «первые пять минут игры», здесь, как мне кажется, замешан в основном фактор удаления игроков. Дело в том, что команды не могут выйти на поле в неравных составах уже в начале первого периода, но с каждой последующей секундой вероятность игры с неравными составами повышается, и к 5 минуте периода приближается к нормальным значениям. А вот во втором и третьем периодах такое возможно с самого начала периода, ведь удаление может остаться с предыдущего периода. Поэтому количество голов, когда составы равны, ниже, а затем, с ростом вероятности возможного удаления игроков, количество голов начинает расти. Также в первые 5 минут счет в матче зачастую равный, поэтому ни одна из команд не испытывает необходимости отыгрываться и бросаться в атаку. Но с каждой следующей минутой вероятность равного счета становится все меньше, соответственно, необходимость одной из команд идти в атаку растет. Думаю, что данные пока все еще достаточно нормальные.

Узнайте о прогнозировании футбола с помощью метода Монте-Карло.

Для всех трех периодов среднее количество голов в минуту за целый сезон составляет 91, 112 и 105 голов соответственно. Я думаю, эти данные отражают естественные этапы хоккейного матча. В первом периоде счета обеих команд еще довольно близки друг к другу, поэтому команды ведут осторожную игру (особенно в первые пять минут). Во втором периоде, когда команды большую часть времени играют уже с неравным счетом, одна команда зачастую вынуждена отыгрываться, а вторая пытается нарастить преимущество. В третьем периоде у команды, которая ведет в счете, осторожность повышается, так как ей необходимо думать уже о сохранности своих ворот, а не о том, чтобы увеличить разницу в счете, поскольку времени до конца матча остается не так уж много и с имеющимся преимуществом команда сможет одержать победу, если не пропустит гол.

Отметим, что без учета последних двух минут игры, в которые забивается очень много голов, за третьи периоды команды в среднем забивают по 96 голов в минуту за рассматриваемый сезон. Однако и эти данные ни на что не влияют.

Что действительно является существенным, так это эффект завершения игры. В последние две минуты третьего периода показатель забитых голов подскакивает примерно до 200% от нормального (напомню, что средняя результативность обеих команд в первые 18 минут составляет 96 голов в минуту за полный сезон). В таблице ниже вы можете видеть, как распределяются 383 гола, забитые за последние две минуты.



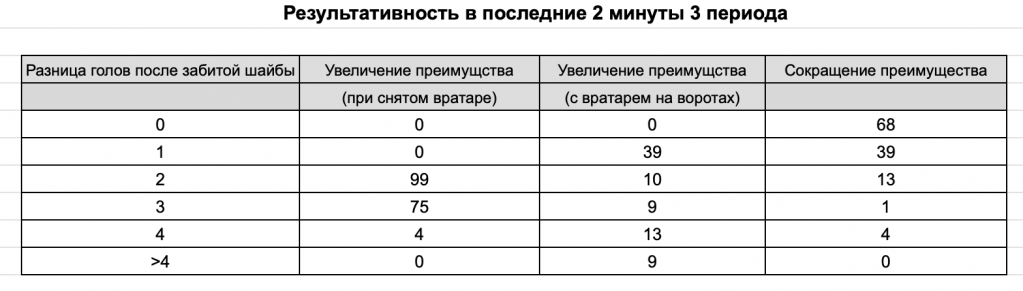
Если бы в процессе подсчета голов не учитывалась бы разница голов, то мы бы ожидали увидеть 96 случаев увеличения преимущества и 96 случаев потери преимущества за последние две минуты игры. Но вместо этого мы наблюдали 125 случаев потери преимущества (130% от нормы) и 258 случаев увеличения преимущества (269% от нормы).

Что еще мы можем узнать из анализа хоккея?

• Что касается случаев увеличений преимущества, 178 из них связаны с ударам по пустым воротам, а остальные 80, забитые с вратарем на воротах, предположительно могут быть связаны с «нормальными» процессами (между прочим, до последних 2 минут было еще 10 ударов по пустым воротам, все из которых увеличили разницу до 3 и более голов). Так что вывод о том, что голы в пустые ворота были на 100% избыточными, вероятно, не лишен оснований. Как видите, команды очень часто позволяют забивать по пустым воротам, проигрывая в 2 и более гола. Анализ проводился на основе данных 2004 года, и с тех пор наблюдается тенденция отводить вратаря, когда разница голов больше (и, как правило, когда остается больше времени). Если такая стратегия дает, скажем, вдвое больше времени с пустыми воротами, шансы на то, что голы пустые, фактически удваиваются.
• Из общего числа сокращений преимущества 68 случаев сравняли счет. Некоторые из этих 68 голов были забиты в равных составах, а некоторые – при снятом вратаре. Далее давайте рассмотрим, что происходит в последние 2 минуты матчей, разница в которых составляет 2 и более шайбы. Только в 4 матчах проигрывающая команда смогла отыграть отставание в 2 гола в последние две минуты. В завершающие моменты игры проигрывающая команда следует одной из двух моделей. Модель №1 – это гол, сокращающий отрыв (со снятым вратарем или нет). Модель №2 – это капитуляция: ведущие в 2 и более шайбы команды забили 31 гол (9+13+9 голов), когда у отстающей команды на воротах был вратарь, чтобы подкрепить крупное (более чем в 2 гола) преимущество. Но в ответ в аналогичной ситуации отстающая команда смогла поразить ворота соперника всего 5 раз, не снимая вратаря (то есть, без дополнительного нападающего). Таким образом, в позднем отрезке игры сила забитых отстающими командами голов уменьшается по мере увеличения разницы забитых голов.

Этот анализ не дает ответа на вопрос, насколько возрастает количество забитых голов в конце третьего периода, когда игра близка к завершению. Все, что здесь можно было сделать – это провести сравнительный анализ результатов в конце игры по сравнению с результатами за предыдущие периоды. Необходимо изучить, насколько успешны все эти попытки команд уменьшить отрыв в конце игры. Причина, по которой этот анализ не был проведен, заключается в том, что данные показатели дополнительных очков меняются от сезона к сезону, поэтому трудно делать какие-то выводы. В 2004 году этот ажиотаж с забиванием голов к завершению игры (в основном по пустым воротам) составлял около 0,1 гола за игру на команду, и их можно приблизительно включить в модель Пуассона. Я расскажу об этом позже.

Момент №2

Второй важный момент – это овертаймы. В плей-офф не допускаются ничьи, но продление игры с целью получить еще один гол разрушает условия Пуассона. Однако их можно точно смоделировать в качестве Пуассоновского процесса, за которым в случае необходимости последует биномиальный процесс.

В регулярном же сезоне, согласно действующим правилам, ничья в соответствии с нормативными требованиями приводит к другому виду овертаймов, команды играют дополнительно до 5 минут. Кроме того, из каждой команды удаляется по одному игроку, что, возможно, влияет на параметр μ, и штраф за поражение отсутствует. Но даже в этом случае овертаймы также можно смоделировать в качестве Пуассоновского процесса, за которым при необходимости последует 3 возможных исхода.

Я еще вернусь к этим двум исключениям позже. Однако данные показывают, что результативность за последнюю минуту и ​​дополнительное время не имеют существенного влияния на Пуассоновский характер оценки в играх регулярного сезона. Ниже представлена ​​таблица, основанная на регулярном сезоне НХЛ 2004 года, с фактическими и ожидаемыми числами (μ = 2,57, среднее количество голов для одной команды за игру в 2004 году) забитых и пропущенных голов.



Глядя на эту таблицу, можно быстро прийти к выводу, что распределение Пуассона довольно хорошо предсказывает распределение голов. Или нет? Чтобы узнать это наверняка, нам необходимо обработать эти данные с помощью критерия хи-квадрат. Данный критерий измеряет отклонения фактических результатов от ожидаемых, выражая общее отклонение в статистических терминах. В нашем случае распределение Пуассона с честью проходит тест хи-квадрат. Отклонения от ожидаемых очень малы, и если вы примените данный тест к другим сезонам, то получите тот же результат: голы – Пуассон.

Итак, мы можем сделать вывод: количество забитых и пропущенных голов в хоккейном матче подчиняется распределению вероятностей Пуассона.

Как Пуассон поможет сделать ставку на хоккей?

Придя к выводу, что забивание голов – это Пуассон, мы можем ответить на большое количество вопросов. В качестве примера рассмотрим шатауты (матчи, в которых команда не пропустила ни одного гола).

Вам не нужен Пуассон, чтобы узнать, что в 2004 году частота шатаутов составила:

193 / (2 x 1230) = 0,078 (Пуассон спрогнозировал 0,077)

Однако Пуассон позволяет вам перевести эти цифры в контекст любого среднего количества голов за игру. В 2004 году команды забивали за игру в среднем 2,57 гола. Ниже приведена таблица вероятностей шатаутов для предполагаемого контекста подсчета голов.




Вы можете видеть, что в начале 1980-х, когда за игру одной командой забивалось в среднем около 4 голов, добиться шатаута было в четыре раза сложнее, чем сегодня. Теперь у вас есть инструмент для сравнения тотала шатаутов от сезона к сезону и во времени.

Почему Пуассон позволяет создавать математические прогнозы на хоккей?

Голы в хоккее – это Пуассон

• Свойство пуассоновского процесса заключается в том, что сумма/среднее значение пуассоновских переменных также является пуассоновским. Если голы в игре – это Пуассон, то и голы за сезон также являются пуассоновскими. Если пойти в обратном направлении, то мы получим вот что: если забитые голы в НХЛ – это Пуассон, то и голы каждой конкретной команды, скорее всего, также будут пуассоновскими. Оказывается, что голы, забиваемые командой – это пуассоновская оценка, хотя, замечу, процесс Пуассона не обязательно должен быть разложен на подпроцессы Пуассона. У каждой отдельной команды, однако, будет свой собственный параметр μ (среднее количество голов за игру) для забитых голов, рассчитанный по некоторому типу распределения вероятностей (возможно, нормального, а может быть и нет). 
• Пропущенные голы на командном уровне также являются Пуассоном. Вероятность того, что Нью-Джерси не пропустит за игру ни одного гола в 2004 году составляла 13,53% (среднее количество пропущенных голов за игру 2,00), а число ожидаемых шатаутов за сезон – 11. По факту же Нью-Джерси зафиксировали за сезон 14 шатаутов. Для Флориды вероятность не пропустить ни одного гола за матч в 2004 году составляла 6,72% (среднее количество пропущенных голов за игру 2,70). Ожидаемое количество шатаутов за сезон у Флориды составляло 5,5, а по факту команда зафиксировала 7 шатаутов. Буффало с таким же ожидаемым показателем зафиксировал только 4 шатаута. У Питтсбурга со средним количество пропущенных голов за игру в 3,70 ожидаемое количество шатаутов составляло 2, а по факту команда зафиксировала за сезон 3 шатаута.

Голы игроков в хоккее – тоже Пуассон

Более того, и индивидуальный показатель забитых голов также, вероятно, будет пуассоновским, и у каждого игрока будет свой параметр μ. Однако на уровне игрока данное утверждение для нас менее полезно. Проблема здесь заключается в следующем: 

• почти для всех игроков μ составляет меньше 1 за одну игру; 
• распределение μ между игроками почти наверняка ненормально (его хвост очень длинный и уходит вправо). 

Тот факт, что μ небольшой, означает, что преобладание вероятности составляет 0 голов в игре с почти всей оставшейся вероятностью на 1 гол в игре. Оценка μ имеет решающее значение для правильного применения распределения Пуассона. На уровне одного матча сложно сделать это правильно для отдельных игроков, но если наша единица времени – сезон, все становится гораздо проще. Рассмотрим результаты Матса Сундина. За 14 сезонов он показал себя как «игрок с 30 гарантированными голами за сезон», забив (с поправкой на травмы) минимум 30 голов в 12 сезонах и в среднем 35 голов за сезон. Пуассон говорит нам вот что: забивая в среднем 35 голов, Матс должен забивать 30 или более голов в 77% случаев (11 из 14 сезонов, что довольно хорошо согласуется с данными). Также Пуассон говорит, что его шансы на 50 голов в сезоне составляют менее 1% (извини, Матс). 

Итак, мы прояснили очень много важных моментов насчет Пуассона, и уже в следующей статье мы с вами рассмотрим, что происходит, когда два Пуассоновских процесса начинают конкурировать. На нашем сайте вы можете узнать больше о прогнозировании других видов спорта: о прогнозировании футбола или тенниса, и даже о прогнозировании баскетбольных матчей. А чтобы не пропустить выход новых материалов, обязательно подписывайтесь на нас в соцсетях (Telegram, VK), на наш канал в YouTube, а также на канал создателя проекта xScore, Артёма Gameleona, из которого был взят данный материал.